Searching for Activation Functions (Ramachandran et al., 2017)

Switching from the ReLU non-linearity, $\text{max}(0, x)$, to Swish, $x \cdot \text{sigmoid}(x)$, consistently improves performance in neural networks across both vision and machine translation tasks.

Update

After prior work came to light that uses the same non-linearity, this paper was updated to focus more on the search process used to investigate the space. One new takeaway for me was how diverse the effective activation functions were (see figures in the new version of the paper).

Original Post

Non-linear functions are the key to the representation power of neural networks. Many different ones have been proposed, though it is difficult to make theoretical claims of their properties and so the choice of which to use is generally empirical. This paper proposes a new non-linearity, $\text{swish}(x) = x \cdot \text{sigmoid}(x)$.

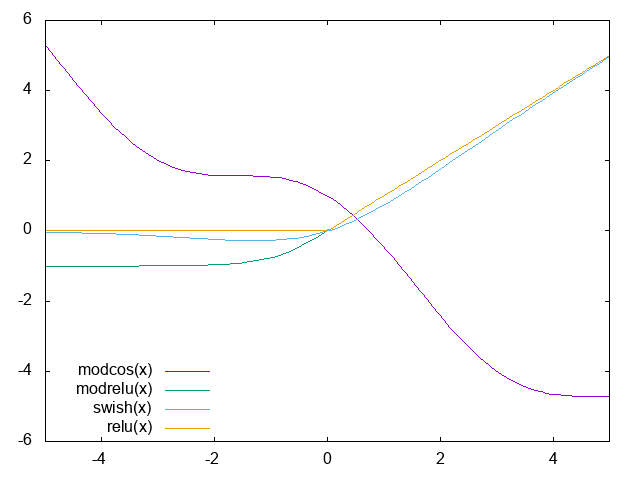
Interestingly, it was chosen by a combination of exhaustive search and search with reinforcement learning across a range of functions, evaluating on CIFAR-10 with a small model. ReLU variants were consistently second-best to swish variants, and generally the more complicated functions performed worse. They do mention two functions that performed well, but didn’t generalise: $\text{cos}(x) - x$ and $\text{max}(x, \text{tanh}(x))$, which look like this:

Four activation functions

In a range of experiments in vision and machine translation swish does at least as well or slightly better than the alternatives. It also seems more robust to network depth and to work across different network structures. As for why it works so well, there are two main ideas: (1) it adds smoothness to the ReLU, (2) it has some sensitivity to negative inputs. Both of these seem particularly important at the start of training.

Citation

ArXiv Paper

@ARTICLE{2017arXiv171005941R,
author = {Ramachandran, P. and {Zoph}, B. and {Le}, Q.~V.},
title = "{Swish: a Self-Gated Activation Function}",
title: "{Swish: a Self-Gated Activation Function}",
journal = {ArXiv e-prints},
archivePrefix = "arXiv",
eprint = {1710.05941},
keywords = {Computer Science - Neural and Evolutionary Computing, Computer Science - Computer Vision and Pattern Recognition, Computer Science - Learning},
year = 2017,
month = oct,
adsurl = {http://adsabs.harvard.edu/abs/2017arXiv171005941R},
adsnote = {Provided by the SAO/NASA Astrophysics Data System}
}